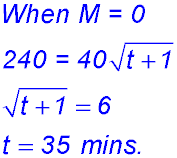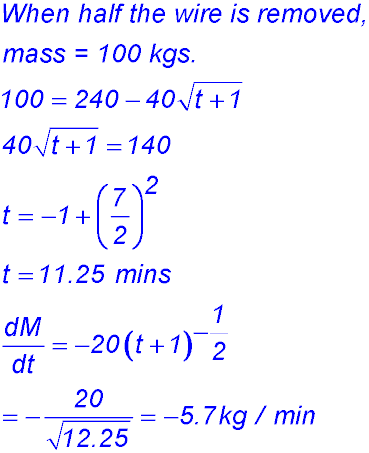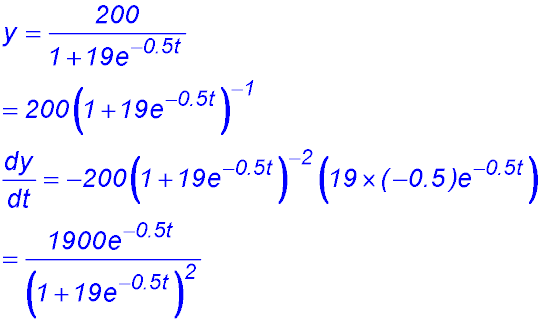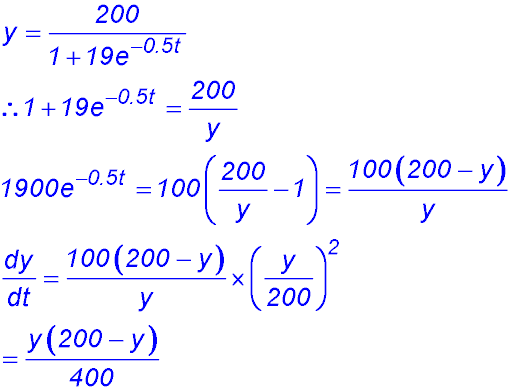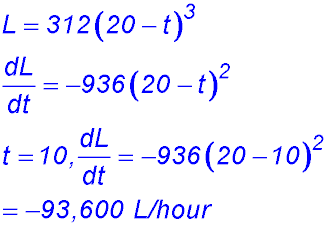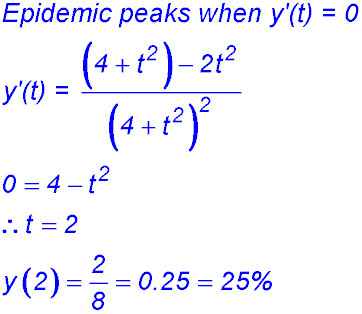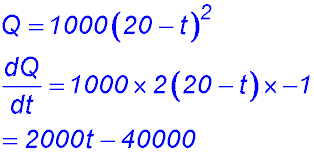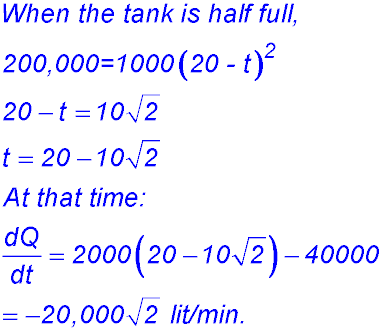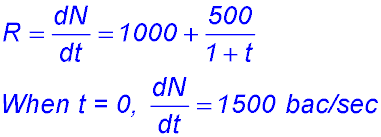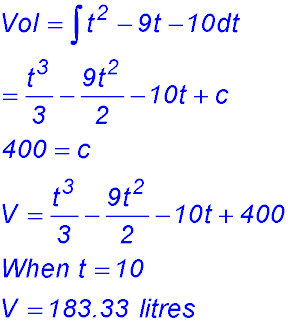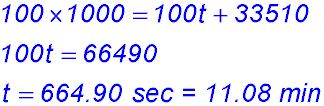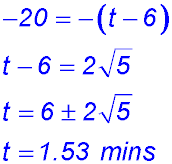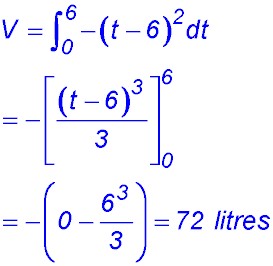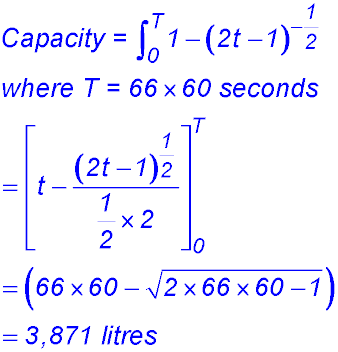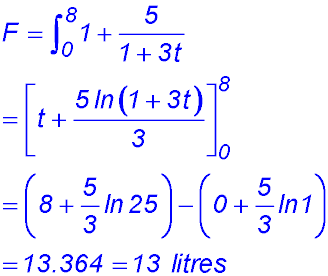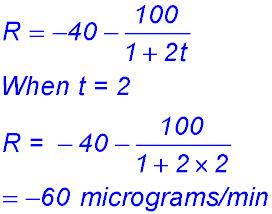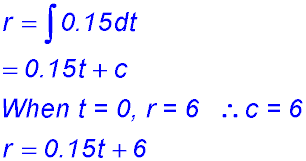Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Applications of Calculus - basic rates of change.
Test Yourself 1 - Solutions.


 

(ii)

Given the quantity. 1. (i) Find the intial mass of the wire on the cylinder.

At t = 0, M = 240 - 40 × 1 = 200 kgs.

(ii) Find the time taken to remove all the wire from the cylinder.

(iii) the rate at which the wire is being removed from the cylinder when half the wire has been removed.
 

2. (i)

(ii)

(iii)

(iv) To obtain the population (y) when the rate is a max, we can simply determine the second derivative. The result has to be a maximum value because the first derivative equation just proved (i.e. the rate) is a negative quadratic in y. We could also find the third derivative (which has a negative coefficient for y).
 

3. (i) When t = 0, L = 312 × 203 = 2.496 million litres - so say 2.5 million (2,500,000) litres.

(ii) When the pool is empty, L = 0 so t = 20 hours.

(iii)

(iv)

  4. (i)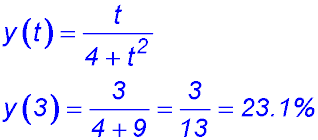

 

(ii)

  5.
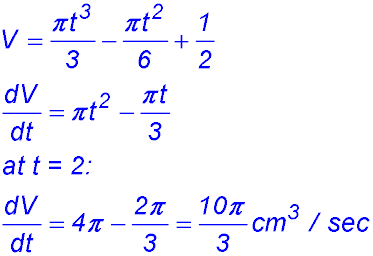  6. (i) Q = 1000(20 - t)2

When t = 0, Q = 400,000 litres.

(ii)

(iii) 2000t - 40,000 = -20,000 (NB: negative - water flowing out).

t = 10 mins.

(iv)

   
   
   
Given the rate. 10. Note: the first step is to replace the R with a rate expression so we do NOT forget we are dealing with the derivative as our starting point.

(i) What is the rate of change in the number of bacteria?

(ii)

NOTE: When t = 0, N = 1500.

As t approaches ∞ N approaches 1000.

 

(iii) total increase in the number of bacteria in first 9 secs:
  11. (i) The largest value of T for which the expression for the rate (R) is physically reasonable:

(ii) the exact amount of water left in the tank once the water stops leaking:
  12. (i)

(ii)

  13. (i)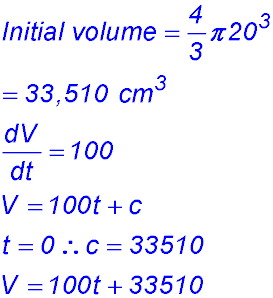

 

(ii)

  14.

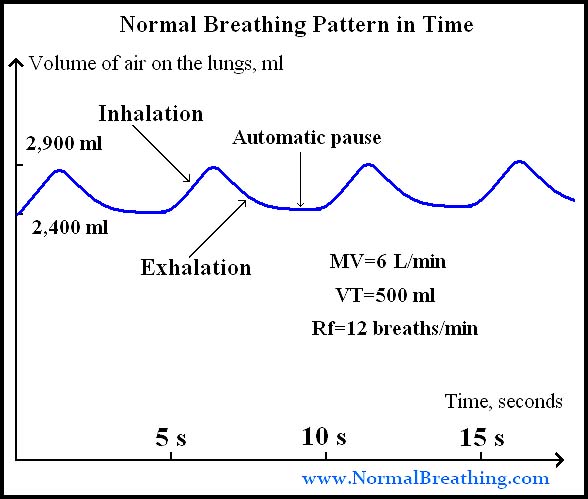
Lung capacity for an adult is about 6 litres. Clearly the lungs can never be full nor empty. We have a residual capacity which increases and decreases as we breathe. The following diagram shows how breathing affects the amount of air in our lungs.

Note that a typical breathing cycle takes about 500 ml of air during one breath.

So how many litres of air did you breath into your lungs while you completed this question?

  15. (i) The initial rate of outflow is 36 litres/minute.

(ii) When R = 0, t = 6 minutes.

(iii)

(iv)

  16.
  17. (i)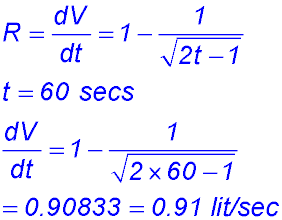

(ii) The rate R < 1 as the 2nd term is being subtracted.

Hence, taking the maximum rate = 1, the tank fills for 66 min at 1 litre/sec. Hence the maximum capacity:

66 min × 60 secs × 1 litre = 3,920 litres.
As R < 1, the capacity must be less than 3,920 litres.

(iii)

  18. (i)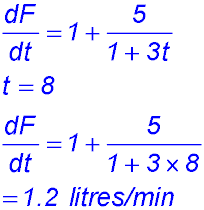

(ii)

 

(iii)

  19. (i) When t = 0, R = -140 μgm/min.

(ii)

(iii) The second term is always positive as t ≥ 0 and that term is subtracted from -40, so the rate cannot ever be higher that -40 μgms/min.

(iv)

 

(v)

(vi) If 140 mgs of venom had been released from the bite, 2.64 mgs have been neutralised in the first hour after the anti-venom was injected. The remaining (140 - 2.64) mgs will be neutralised at the rate of

40 μgm/minute = 0.04 mgs/minute.

So the venom should be all neutralised after another 57.23 hours - that is just less that 2½ days after the anti-venom injection is given.
  20. (i)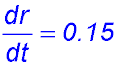

(ii)

(iii) When t = 8, r = 0.15×8 + 6 = 7

∴ A = 49π cm2.